[科普中国]-古津串行

古津串行又称为古津序列（Gysin sequence），是一种特殊的正合列。

简介古津串行又称为古津序列，是一种特殊的正合列。

对于任意的定向实n维向量丛ξ，存在整数系数的形如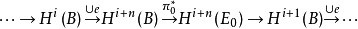的正合列，其中π0:E0→B（E0为全空间E的非零向量组成的空间），e为ξ的欧拉类，∪e代表同态a↦a∪e(ξ)，这个正合列被称为古津序列。1

正合列(exact sequence)

正合列是一类特殊的群正合列。

若环同态f:R→T为满同态且R,T分别有理想A,B使在f之下A,B的元素是一一对应的（即切除引理条件成立），则有群正合列：

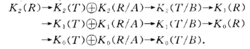
欧拉类欧拉类是实向量丛底空间的一个上同调类。

定向实n维向量丛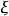的欧拉类是上同调类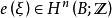，在标准同构

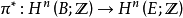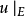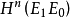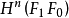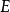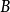下，它对应于，其中u是中惟一的上同调类，限制在中是标准的定向类。这里的为全空间，为底空间。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学