旅行售货员问题(travelling salesman problem)是一类组合最优化问题,设有一个售货员从城市1出发,到城市2,3,…,n去推销货物,最后回到城市1.假定任意两个城市i,j间的距离dij(dij=dji)是已知的,问他应沿着什么样的路线走,才能使走过的路线最短?容易看出,中国邮递员问题要求走遍所有“线”,而后者要求走遍所有“点”,旅行售货员问题就是在一个完全网络中,找出一个具有最小权的哈密顿圈,寻求旅行售货员问题的有效算法似乎是没有希望的,它属于NP完全类,一个可行的办法是首先求一个哈密顿圈,然后适当修改,以得到具较小权的另一个哈密顿圈,旅行售货员问题有着明显的实际意义,除售货员之外,邮局里负责到各个信箱取信的邮递员,以及去各个分局送邮件的汽车等都会类似地遇到这个问题,还有一些问题表面上似乎与之无关,而实质上却可以归结为旅行售货员问题求解,如计算机线路问题、无中间存储的工件加工问题等1。
基本介绍设有p个城镇,已知每两个城镇之间的距离,一个售货员从某一城镇出发巡回售货,问这个售货员应如何选择路线,能使每个城镇经过一次且仅一次,最后返回到出发地,而使总的行程最短?这个问题称为旅行售货员问题。容易看出,旅行售货员问题就是在一个赋权完全图中找一个具有最小权的Hamilton圈,我们称这种圈为最优Hamilton圈。
除旅行售货员问题之外,邮局中负责到各个信箱取信的邮递员,以及去各个分局送邮件的汽车等都会类似遇到这种问题,还有一些问题表面上似乎与之无关,而实质上却可以归结为旅行售货员问题来解决,既然这个问题有着如此广泛的应用,那么找一个求解最优Hamilton圈的有效算法就成为一件非常重要的事2。
问题解法目前还没有一个求解最优Hamilton圈的有效算法,所以希望有一个方法以获得相当好(但不一定是最优)的解,下而我们给出一个较好的近似算法——最邻近算法,以及一个修改的方法。
设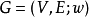 是一个赋权完全图,根据实际问题,我们可作如下的规定:对
是一个赋权完全图,根据实际问题,我们可作如下的规定:对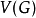 中任何三个顶点
中任何三个顶点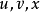 ,满足
,满足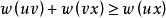 。
。
求近似最优Hamilton圈的最邻近算法:
(1) 任选一个顶点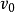 作为起点,找一条与
作为起点,找一条与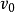 关联其权最小的一条边e1,e1的另一个端点记为v1,得一条路
关联其权最小的一条边e1,e1的另一个端点记为v1,得一条路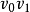 ;
;
(2)设已选出路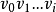 ,在
,在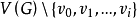 中取一个与vi最近的相邻顶点
中取一个与vi最近的相邻顶点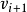 ,得
,得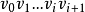 ;
;
(3)若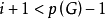 ,用i代i+i返回(2),否则记
,用i代i+i返回(2),否则记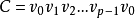 ,停止。
,停止。
最后所得的C就是G的一个近似最优的Hamilton圈。
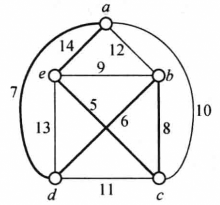
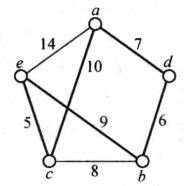
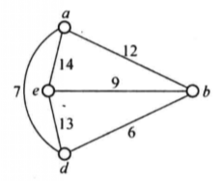
例如,在图1中,粗边表示了起点选a并用最邻近法求得的一个Hamilton圈C=adbcea,该Hamilton圈的长度为40。2
用最邻近法求得的Hamilton圈一般不是最优的,但通过以下的修改可获得更短的Hamilton圈,其修改方法如下:
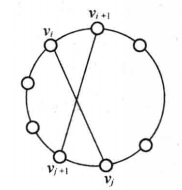
设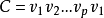 是G的一个Hamilton圈,若存在i,j适合
是G的一个Hamilton圈,若存在i,j适合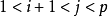 ,并且
,并且
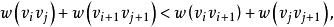 则Hamilton圈
则Hamilton圈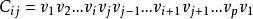 (它是由C中删去边
(它是由C中删去边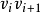 和
和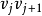 ,添加边
,添加边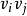 和
和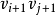 而得到的(如图2所示))的权和
而得到的(如图2所示))的权和
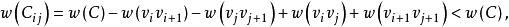 因而Hamilton圈
因而Hamilton圈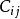 将是C的一个改进。
将是C的一个改进。
在接连进行上述的一系列修改后,最后得到的一个Hamilton圈不能再用此方法改进了,这个Hamilton圈虽然未必是最优的,但有理由认为它常常是比较好的2。
例如,用最邻近法得到的图1所示的G的Hamilton圈为C=adbcea,用此方法修改后可得C'= acebda(见图3),其长度为37。
我们可以利用Kruskal算法给出最优Hamilton圈下界的一个估计式,设v是赋权完全图G的任意一个顶点,用Kruskal算法求出G-v的一棵最优树T,设C是G的一个最优Hamilton圈,显然C-v是G-v的一棵生成树,因此
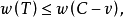 设G中与v关联且权最小和权次小的两条边分别是e和f,则
设G中与v关联且权最小和权次小的两条边分别是e和f,则
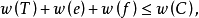 因此
因此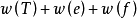 将是G的最优Hamilton圈的一个下界估计式。以图1中的G为例,G-c的图为图4(a)所示,用Kruskal算法求得G-c的一棵最优树T(如图4(b)所示),T的权为22,G中与c关联而权最小的两条边为ce和西cb,因此G的最优Hamilton圈C满足
将是G的最优Hamilton圈的一个下界估计式。以图1中的G为例,G-c的图为图4(a)所示,用Kruskal算法求得G-c的一棵最优树T(如图4(b)所示),T的权为22,G中与c关联而权最小的两条边为ce和西cb,因此G的最优Hamilton圈C满足
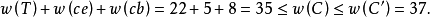
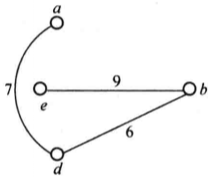
由此可见,结合上面两个方法所得到的Hamilton圈是一个较好的近似解,其实C'就是图1所示的图G的一个最优Hamilton圈2。
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国