戴德金η函数是定义在上半平面的全纯函数,这是权1/2的模形式之一例。
简介戴德金η函数是定义在上半平面的全纯函数,这是权1/2的模形式之一例。
对每个属于上半平面的复数τ,置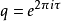 ,则η函数表为
,则η函数表为
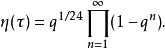
η函数满足以下函数方程:
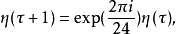
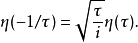 此处的根号是方根函数在右半平面的解析延拓
此处的根号是方根函数在右半平面的解析延拓
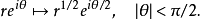
一般而言,对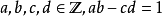 ,我们有
,我们有
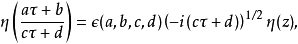 其中的自守因子
其中的自守因子 定为
定为
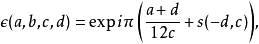 而
而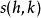 为戴德金和
为戴德金和
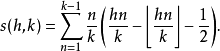
由此函数方程可知η是权1/2的模形式,因此可由η构造更多的模形式,例如魏尔施特拉斯的模判别式即可表为
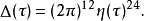
事实上,由函数方程可知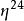 是权12的模形式,而这类模形式构成复一维向量空间,比较傅里叶展开的常数项,上式立可得证。1
是权12的模形式,而这类模形式构成复一维向量空间,比较傅里叶展开的常数项,上式立可得证。1
全纯函数全纯函数(holomorphic function)是复分析研究的中心对象;它们是定义在复平面C的开子集上的,在复平面C中取值的,在每点上皆复可微的函数。这是比实可微强得多的条件,暗示著此函数无穷可微并可以用泰勒级数来描述。
解析函数(analytic function)一词经常可以和“全纯函数”互相交换使用,虽然前者有几个其他含义。全纯函数有时称为正则函数。在整个复平面上都全纯的函数称为整函数(entire function)。“在一点a全纯”不仅表示在a可微,而且表示在某个中心为a的复平面的开邻域上可微。双全纯(biholomorphic)表示一个有全纯逆函数的全纯函数。1
模形式在数学上,模形式是一种解析函数,这种函数的只接受来自复数平面内上半平面中的值,并且这种函数在一个在模型群的群运算之下,会变成某种类型的函数方程,并且通过函数计算出的值也会呈现出某个增长趋势。模形式理论属于数论的范畴。模形式也出现在其他领域,例如代数拓扑和弦理论。
模形式理论是更广泛的自守形式理论的特例。自守形式理论的发展大致可分成三期:
19世纪初:探讨与椭圆函数相关的方面。
19世纪末:此时单变数自守形式的概念诞生。此理论由菲利克斯·克莱因等人发展。
1925至1960年:由赫克发端,发现了模形式与数论的联系。1
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国