[科普中国]-线性化重力

线性化重力是广义相对论中的近似方案，其中忽略了时空度量的非线性贡献，简化了对许多问题的研究，同时仍然产生了有用的近似结果。

方法在线性化引力1中，度量张量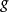 被视为爱因斯坦方程（通常是明科夫斯基时空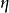） 和扰动的精确解 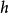的总和。

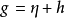
其中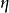 是非动态背景指标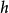， 表示真实度量的偏差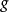（ ）从平时空间。

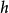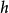使用微扰理论的方法处理扰动，通过忽略高于1的所有有序项来“线性化”（二次方的） ，三次的 等...

在爱因斯坦场方程（EFE），是非线性的度量，都难以精确地解决和上述扰动方案允许获得线性化爱因斯坦场方程。这些方程在度量中是线性的，并且线性化EFE的两个解的总和也是解决方案。因此，“忽略非线性部分”的想法被封装在该线性化过程中。

该方法用于导出牛顿限制，包括第一校正，很像的存在推导引力波导致，后量化，以引力。这就是为什么线性化引力的概念方法是粒子物理学中的规范方法，弦理论，更普遍的是量子场理论，其中经典（玻色子）场表示为粒子的相干态。

这种近似也称为弱场近似，因为它仅在扰动h非常小时才有效。

弱场近似在弱场近似中，规范对称性与具有小“位移”的微分同胚相关（具有大位移的微分同胚明显违反弱场近似），其具有精确形式（对于无穷小变换）

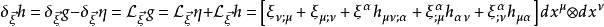
其中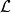 是Lie导数，我们使用η不变换的事实（根据定义）。注意，我们相对于η而不是g提高和降低指数，并且相对于η采用协变导数（Levi-Civita连接）。这是线性化重力的标准做法。线性化引力的思维方式是：背景度量η是度量，h是使用该度量在时空上传播的字段。

在弱场限制中，这种规范转换简化为

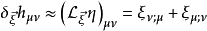
弱场近似在寻找某些常数的值时很有用，例如在爱因斯坦场方程和Schwarzschild度量中。

线性化爱因斯坦场方程该线性化爱因斯坦场方程（线性EFE）是一个近似爱因斯坦场方程，其有效期为弱引力场，用来简化在许多问题广义相对论和讨论的现象引力辐射。近似也可以用来推导牛顿引力作为爱因斯坦引力的弱场近似。

通过假设时空度量仅与某个基线度量（通常是Minkowski度量）略有不同来获得等式。然后，度量的差异可以被视为基线度量上的字段，其行为由一组线性方程近似。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所