[科普中国]-模糊聚类法

把模糊数学方法引入聚类分析即产生了模糊聚类分析方法。模糊聚类分析方法大致可分为两种：一是基于模糊关系上的模糊聚类法．并称为系统聚类分析法。另一种称为非系统聚类法，它是先把样品粗略地分一下，然后按其最优原则进行分类，经过多次迭代直到分类比较合理为止，这种方法也称为逐步聚类法。我们通常讲的模糊聚类分析是指将模糊数学的原理应用到系统聚类分析的方法。模糊聚类分析的步骤：(1)确定聚类单元全集U；(2)确定聚类准则和聚类因子；(3)根据聚类准则及因子进行数据的调查与整理；(4)将统计数据进行元量纲处理．称为正规化1。

什么是模糊聚类法在经济学、社会学、生物学、气象学、医药等许多领域的研究中，经常遇到处理具有模糊性的数据问题。这里所谓的模糊性，主要是指客观事物差异的中间过渡中的“不分明性”和“边界不清”的意思，例如商品评价中“质量好、比较好、比较差等”，气象灾害对农业产量的影响程度为“严重、重、轻”，病人患某种疾病的症状是“重、轻”以及“有矿与无矿”，“冷、暖”“多云间晴”都难以明确地划清界限。

为了研究这方面的问题，1965年由美国自动控制专家查德(L.A.Zadeh)首先提出模糊集合的概念，之后成功的用数学方法描述模糊概念，从而产生了模糊数学。从模糊数学的诞生到现在也仅有几十年的历史，其理论尚不十分完善，但是这门科学的发展非常迅速，模糊数学应用的触角已伸人到国民经济领域的各个学科。模糊数学的理论基础是模糊集理论，下面介绍模糊集理论应用到聚类分析中从而产生了模糊聚类法2。

模糊聚类的基本概念特征函数对于一个普通的集合E，空间中任一元素x要么有x∈E，要么有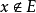 ，二者必居其一，这一特征用·个函数表示为

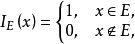
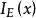称k(z)为集合E的特征函数2。

例如，设E为某地区在某年度完成国家利税的企业全体，这时对该地区任一企业x，我们可用特征函数描述它是否完成了国家利税，即

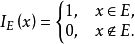
隶属函数与模糊集如果我们进一步描述某企业完成国家利税的程度大小时，仅用特征函数就不够了。模糊集理论变将特征函数的概念推广到[0，1]内取值的函数以度量这种程度的大小，这个函数称为集合E的隶属函数，记为E(x)，即对于每一个元素x，有[0，1]内的一个数E(x)与之对应2。

若在集合E上定义了一个隶属函数，则称E为模糊集。

模糊矩阵及其褶积(1)若矩阵A的各元素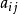 满足0≤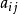 ≤1，则称A为模糊矩阵2。

(2)设A=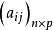 和B=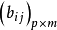 为两个模糊矩阵，令

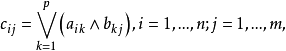则称矩阵C= 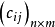为模糊矩阵A与B的褶积，记为C=AB。

其中“∨”和“∧”的含义为：a ∨b=max{a，b}， a ∧ b=min{a，b}。

显然，两个模糊矩阵的褶积仍为模糊矩阵。

模糊等价矩阵及其λ截阵设方阵A为一模糊矩阵，若A满足

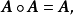则称A为模糊等价矩阵。

模糊等价矩阵可以反映模糊分类关系的传递性，即描述诸如“甲像乙，乙像丙，则甲像丙”这样的关系。

设A=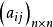为一个模糊等价矩阵，0≤λ≤1为一个给定的数，令

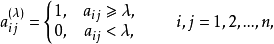则称矩阵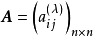为A的λ-截阵2。

模糊聚类方法具体步骤如下：

(1)计算相似系数矩阵R或样品的距离矩阵D2。

(2)将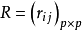(或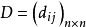中的元素缩到0与1之间形成模糊矩阵，我们统一记为A=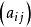，例如对相似系数矩阵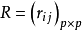，可令

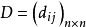
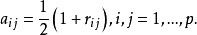对于距离矩阵，可令

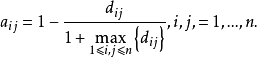
(3)建立模糊等价矩阵

一般说来，上述模糊矩阵A=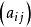不具有等价性，这可以通过模糊矩阵的褶积将其转化为模糊等价矩阵，具体方法如下：

计算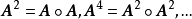，直到满足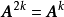，这时模糊矩阵Ak便是一个模糊等价矩阵。记。

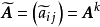(4)聚类

将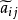按由大到小的顺序排列，从λ=1开始，沿着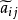由大到小的次序依次取λ=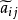，求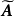的相应的λ-截阵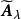，其中元素为1的表示将其对应的两个变量(或样品)归为一类，随着λ的变小，其合并的类越来越多，最终当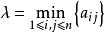A=min{a。)时，将全部变量(或样品)归为一类。2

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所