[科普中国]-二阶形式语言

二阶形式语言可以在一阶形式语言的基础上构成，“一阶”和“二阶”都是最初由弗雷格提出的概念。在二阶语言中，函词f或谓词p都由量词进行了约束，形成了Qf或Qp表达式(Q是一阶量词)，或者，函词f或谓词p都是自身的操作对象，形成ff(xi)或pp(xi)表达式，于是构成了“二阶”特征。

基本介绍一阶形式语言的定义定义1 一阶形式语言由以下部分构成。

(1)字符表

个体变元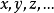：，或者。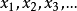

常元：。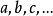

函数符号：。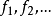

谓词符号：。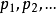

特殊谓词符号：=。

逻辑联结词：。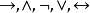

量词：。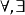

括号：(，)。

(2)形成规则

①项的形成规则：

(i) 任一个体变元，任一常项变元c都是一个项。

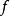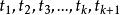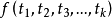(ii) 若是一个带k个自变元的函词，是项，则是一个项。

(iii)只有由定义(i)~(ii)归纳定义得到的字符串是项。

②公式的形成规则：

(i)若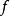是一个带k个自变元的函词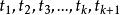，是项，则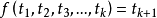是一个公式。

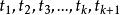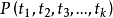(ii)若p是一个带k个自变元的谓词，是项，则是一个公式。

(iii)若A，B是公式，则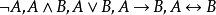是公式。

(iv)若A是公式，是一个变元，则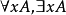是公式。

(v)只有由(i)~(iv)归纳定义得到的字符串是公式。

(3)语句形成规则

如果公式A不含任何自由变元，则是A语句。上述结构构成一阶语言。

(4)给定一阶语言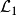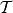，是一个一阶理论，如果它包括：

①谓词演算的所有公理；

②一个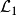中语句组成的集合，有穷或者无穷，它们构成非逻辑公理；

③谓词演算的所有推理规则。

(5)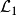中的一个语句A是理论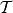的一个定理，如果A是(4)中的①或②语句，或者是以逻辑公理或非逻辑公理为前提，使用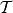的推理规则得到的语句。

(6)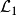中的一个结构(或称模型)M由一个论域D及一阶公式的变元的解释V所组成的非空集合构成，记作：

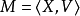对于项；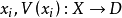

对于函词；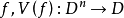

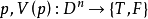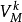对于谓词，用或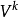表示V的某一次(个)映射，如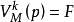表示V的第k次(个)映射使p为假。

一阶形式语言相关重要概念定义如下：

一阶命题变元的解释是对(项或谓词或函词)变元的一个赋值(实例化)。

有量词约束的公式称为量化公式。

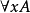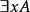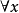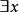对一个量化公式(或)，称其子公式A是量词(或)的辖域。

在公式A中，一个变项如果出现在某个形如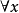(或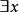)的量词的辖域中，或它就紧跟在∀(或∃)后面，则称在A中的这处出现是约束的。变项的非约束的出现，称为自由出现。

如果在A中有一处自由出现，则称是A中的自由变项。如果在A中的所有出现都是约束的，则是A中的约束变项。

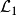是形式化的，也是语法化的，即按照这些符号和句法规则可以或接近构成或验证一个一阶语言的证明系统。

二阶形式语言的定义对于一阶形式语言的定义，对“(2)形成规则”中的“②公式的形成规则”增补如下：若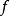和p是一阶函词和一阶谓词，则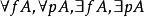是公式。由此构成的语言即二阶形式语言。

相应地，对于一阶形式语言的定义的(4)、(5)、(6)条，即关于理论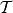、语句A、结构(模型)M，也改称为二阶的。

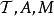二阶算术公理系统定义2 ACA是二阶算术公理系统，它包括PA的公理，另加概括公理(Arithmetical Comprehension Axiom，ACA)，其命题如下：

(1)

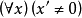
(2)

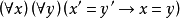
(3)

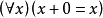
(4)

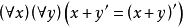
(5)

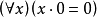
(6)

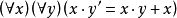
(7)

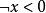
(8)

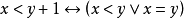
归纳公理：

(9)

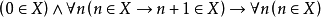
概括公理：

(10)

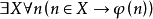
其中：X不在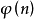中自由出现。

其中，第(10)条概括公理是完全概括模式，即所有满足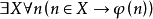公式的闭集。

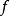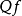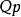“一阶”和“二阶”都是最初由弗雷格提出的概念。在二阶语言中，函词或谓词p都由量词进行了约束，形成了或表达式(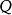是一阶量词)，或者，函词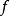或谓词p都是自身的操作对象，形成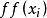或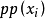表达式，于是构成了“二阶”特征。特别地，在定义2第(9)条中，表达个体属于集合的“属于”符号∈相当于谓词符号p(或函词符号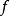)；当一个集合表达式X语义是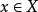，而X是可量词约束的，这相当于量词约束了∈X，或者也可以将X理解成“属于集合”这一谓词，因此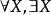构成了量词约束p或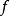，即成为“二阶”语言表达。事实上，一旦语言中出现量词约束的集合，而集合是附有定义的(集合的定义可能带来悖论)，因此，集合出现在表达式确实不能仅仅作为(直觉性的)个体来理解，必须考虑到它的谓词(函词)的意义，即考虑到它和一阶语言的特征还是有本质差别的。对于定义2的第(9)条归纳公理，严格的表达应该是

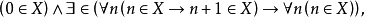即存在着关系∈，使得归纳公理成立。因为n是无穷的，关系是不是无穷的在定义2的第(9)条归纳公理中并未陈述。当补足这一陈述时就产生了二阶语言表达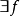。因此，

对于无穷归纳，一般视为二阶语言表达，因此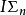，或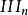模式被视为二阶公理理论(方法)。鉴于定义2的第(8)、(9)两条陈述的二阶语言表达特征，ACA是二阶算术公理系统；当然在这个意义上说，PA也是二阶算术公理系统1。

弗雷格弗雷格(Friedrich Ludwig Gottlob Frege1848～1925)是德国著名数学家、逻辑学家、现代逻辑的创始人， 也被公认是语言哲学和分析哲学的创始人。1848年生于德国魏玛， 1869～1871年先后在耶拿大学和哥廷根大学学习数学、物理学和哲学， 1873年获哥廷根大学博士学位，1874年在耶拿大学数学系任教， 1879年起任数学教授，直至1918年退休。其主要著作有《概念文字：一种模仿算术语言构造的纯思维的形式语言》(1879)、《算术的基础：对数这个概念所作的逻辑的和数学的研究》 (1884)、《算术的基本法则》(第一卷，1893;第二卷，1903)。重要的论文有： “函数和概念”(1891)、“论概念和对 象”(1892)、“论意义和意谓”(1892)。 其中《概念文字：一种模仿算术语言构造的纯思维的形式语言》是弗 雷格思想体系的坚实基础，它提供了一种形式语言和一个一阶谓词演算系统。在此基础上，弗雷格向着 两个方向展开了他的工作：试图从逻辑推出数学，即用逻辑方法定义 数的概念，建立算术的形式系统；试图探讨逻辑哲学，即把概念文字 扩展到自然语言中句子的分析，建立逻辑哲学体系。在逻辑学方面， 其研究的主要目的在于为数学制定 坚实的逻辑基础。他将心理的东西 和逻辑的东西、主观的东西和客观 的东西严格区别开来，批判了逻辑 学中的心理主义学派。不能用心理的过程来解释逻辑的概念、规律， 用心理的东西也不能说明逻辑和数 学的客观性、独立性和普遍性，充 分重视数学与逻辑的密切关系。概 念是某些特殊类型的抽象实体，概 念词是指称这些概念的语言表达式， 要理解意义的性质必须要考察在语 言的使用中所发现的某些客观的特 征。他反对传统逻辑把一切语句都 看成具有主-谓形式的观点，而用 专名和概念词的区别来代替主词和 谓词的区别。概念是判断的谓词， 专名是判断的主词，不能将二者混 同使用。正如函数有不同的阶一样， 概念也有一阶概念和二阶概念之分， 混淆了这种区分，就会产生无意义 的命题。在语言哲学方面，他指出 决不可孤立地寻问一个词的意义， 而只能在一个命题的前后关系中寻 问词的意义，即在语句的语境中才 能确定词的意义。语言运用的基本 单位是句子，只有把单个语词看成 是有助于句子的形成和使用时，才 能理解其意义。他对语境的重要性 的强调，对后期维特根斯坦及日常 语言学派有重要的影响。 自然语言 并不完善，应建立一种逻辑上完善 的语言，他所创造的那个形式化逻 辑系统就是这种语言的一种形式。 弗雷格的另一突出贡献在于首次区 分了含义和指称。一个命题具有三 个因素：名称、指称和含义。两个 专名可能具有不同含义，而具有相 同指称。同一种含义在不同语言中， 甚至在同一种语言中，具有不同的 表述。我们在把握一个语词的含义 时，不一定能同时掌握它的指称。 另外，有些语句可能只具有意义而 无指称，如神话中的语句。我们既 不能只考虑语句的意义，也不能只 考虑语句的指称，而必须将二者结 合起来。在制定数学的逻辑基础的 过程中，弗雷格创立了数理逻辑， 为以后的分析哲学家提供了有用的 分析问题的工具，提出的一些具有 逻辑-语言性质的哲学问题，也为 分析哲学奠定了基础，他的语言哲 学思想对分析哲学关于意义问题的 探讨发生了重要影响。他被公认为 是分析哲学的思想先驱。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学