[科普中国]-里奇标量

在黎曼几何中，数量曲率（Scalar curvature）或里奇标量（Ricci scalar）是一个黎曼流形最简单的曲率不变量。对黎曼流形的每一点，数量曲率是由该点附近的内蕴几何确定的一个实数。

简介在黎曼几何中，数量曲率（Scalar curvature）或里奇数量（Ricci scalar）是一个黎曼流形最简单的曲率不变量。对黎曼流形的每一点，数量曲率是由该点附近的内蕴几何确定的一个实数。

在 2 维数量曲率完全确定了黎曼流形的曲率；当维数 ≥ 3，曲率比数量曲率含有更多的信息。参见黎曼流形的曲率中完整的讨论。

数量曲率一般记为S（其它记法有Sc,R），定义为关于度量的里奇曲率张量的迹：

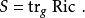
这个迹和度量相关，因为里奇张量是一个 (0,2) 型张量；必须将指标上升得到一个 (1,1) 型张量才能取迹。在局部坐标中我们可以写成

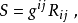这里

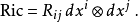给了一个坐标系与一个度量张量，数量曲率可以表示为：

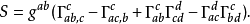
这里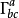是度量的克里斯托费尔符号。

不像黎曼曲率张量或里奇张量可以对任何仿射联络自然地定义，数量曲率只在黎曼几何存在；其定义与度量密不可分。1

传统记法[编辑]在使用张量指标记法的作者中，字母R通常表示三种不同的东西：

1.黎曼曲率张量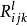：或；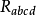

2.里奇张量：；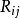

3.数量曲率R。

这三个由它们的指标数目区分开：黎曼张量有四个指标，里奇张量有两个指标，里奇数量曲率没有指标。不使用指标记法的一般将R保留为全黎曼曲率张量的记号。2

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学