[科普中国]-配对函数

在数学中，配对函数是唯一编码两个自然数到一个单一的自然数的过程。在集合论中可以用任何配对函数来证明整数和有理数有同自然数相同的基数。

定义配对函数是双射函数：

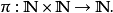
康托尔配对函数康托尔配对函数是配对函数：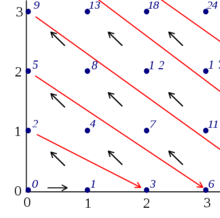

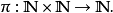
定义为：

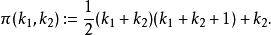
在应用配对函数到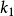和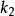的时候，我们经常指示结果的数为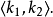

这个定义可以归纳一般化为康托尔元组函数：

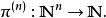
作为：

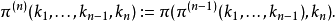
反转康托尔配对功能让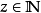是一个任意的自然数。证明存在的价值：

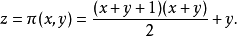因此π是可逆的。在计算中定义一些中间值是有帮助的：

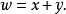
其中t是w的三角形数。如果我们解二次方程：

得到：

当t是非负实数时，这是一个严格递增和连续的函数。

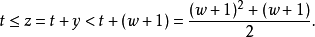可以得到：

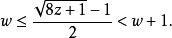因此：

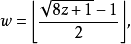其中⌊⌋是高斯符号。可以得到：

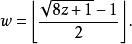
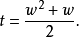
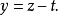
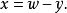
本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学