[科普中国]-克莱罗方程

定义

形如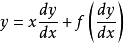 的方程，称为克莱罗微分方程，这里 f 是连续可微函数。1

克莱罗方程的通解具有形式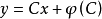：（直线族），此外存在奇解（包络），其中奇解可以通过方程组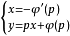：消去参数 p 而得到。2

方程求解方程的通解克莱罗方程的通解可以通过令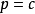（任意常数），代入原方程中求得。3

具体求解步骤已知方程：，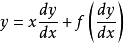

对上式左右两端同时对 x 求导，并令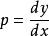，可得：；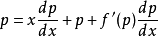

即有：。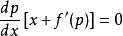

（1）如果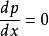，则得到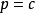，将其代入到式子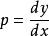中可得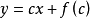：，其中 c 为任意常数，这就是原方程的解。

（2）如果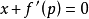 ，则将该式与原方程联立，得到方程组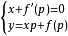： ，消去 p 则得到方程的一个解。求此解的过程与求包络的过程是一致的。不难验证，此解正是通解的包络。由此，克莱罗微分方程的通解为一直线族，即在原方程中以 c 代 p，且此直线族的包络是方程的奇解。1

典例例1求解方程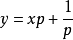 ，其中 。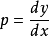

解：这是克莱罗方程，因而易得其通解为，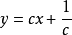

从方程组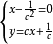 中消去 c，得到奇解：。

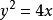方程的通解是直线族，而奇解是通解的包络。1

例2解方程 。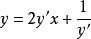

解：令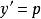 ，则有。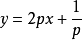

微分后，以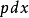代替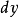，我们得到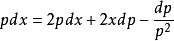：或者。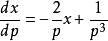

求解这个线性方程后，我们有： 。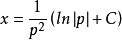

因此，得到：，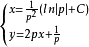

为了求出奇积分，按照一般规则做出方程组： ， ，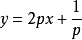

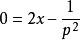由此得到： ，。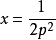

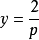所以有：。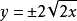

把 y 代入原方程，可知得到的函数并不是解，因此原方程没有奇积分。2