[科普中国]-吉布斯现象

简介

吉布斯现象（又叫吉布斯效应）：将具有不连续点的周期函数（如矩形脉冲)进行傅立叶级数展开后，选取有限项进行合成。当选取的项数越多，在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时，该峰起值趋于一个常数，大约等于总跳变值的9%。

历史起源数学界有过一场“正弦曲线能否组合成一个带有棱角的信号”的争议，这场争议的男主角分别是傅里叶和拉格朗日。

直到1898年，美国人阿尔伯特·米切尔森做了一个谐波分析仪， 当他测试方波时惊讶的发现方波的XN(t)在不连续点附近部分呈现起伏，这个起伏的峰值大小似乎不随N增大而下降！于是他写信给当时著名的数学物理学家吉布斯，吉布斯检查了这一项结果，随即发表了他的看法：随着N增加，部分起伏就向不连续点压缩，但是对任何有限的N值，起伏的峰值大小保持不变，这就是吉布斯现象。

吉布斯现象示意图如下图所示。

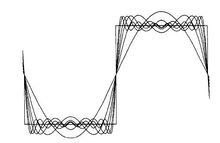
Gibbs 现象解释图像的傅里叶变换 ，由于其变换本身有多种成熟的快速算法（FFT算法），而且性能接近于最佳，从而获得较早的也比较广泛的研究。它的不足之处在于：相邻子图像数据在各个边界不连续造成的所谓Gibbs现象。这是由于图像数据的二维傅里叶变换实质上是一个二维图像的傅立叶展开式。这个二维图像应被认为是周期性的。由于子图像的变换系数在边界不连续 ，而将造成复原的子图像在其边界也不连续 。于是由复原子图像构成的整幅复原图像将呈现隐约可见的以子图像尺寸为单位的方块状结构，影响整个图像质量 。当子图像尺寸较小时更为严重。

解决方法解决这个Gibbs现象的方法是后来研究出来的二维余弦变换（DCT）代替二维傅立叶变换。基本思路为：用一个对称的2N*2N 像素的子图像代替原来N*N 子图像。由于对称性， 子图像作二维傅立叶变换，其变换系数将只剩下实数的余弦项。这样，即可消除Gibbs现象。

应用概述当体系发生变化时，G也随之变化。其改变值△G，称为体系的吉布斯自由能变，只取决于变化的始态与终态，而与变化的途径无关：△G=G终一G始 按照吉布斯自由能的定义，可以推出当体系从状态1变化到状态2时，体系的吉布斯自由能变为：△G=G2一Gl=△H一△(TS) 对于等温条件下的反应而言，有T2=T1=T 则 △G=△H一T △S 上式称为吉布斯一赫姆霍兹公式（亦称吉布斯等温方程）。由此可以看出，△G包含了△H和△S的因素，若用△G作为自发反应方向的判据时，实质包含了△H和△S两方面的影响，即同时考虑到推动化学反应的两个主要因素。因而用△G作判据更为全面可靠。而且只要是在等温、等压条件下发生的反应，都可用△G作为反应方向性的判据，而大部分化学反应都可归人到这一范畴中，因而用△G作为判别化学反应方向性的判据是很方便可行的。[1]

作为判据应用化学反应自发性判断： 考虑ΔH和ΔS两个因素的影响，可分为以下四种情况 1)ΔH0;ΔG0,ΔS0正向非自发 3)ΔH>0,ΔS>0;升温至某温度时，ΔG由正值变为负值，高温有利于正向自发 4)ΔH